유한 오토마타의 구성
유한 오토마타는 위 5가지 항목으로 구성된다.
Q
Q는 유한 오토마타가 가진 상태의 집합이다.
상태의 개수는 유한하므로, Q의 원소 개수도 유한하다.
보기의 예시로 유한 오토마톤은, off와 on 두가지 상태가 Q의 원소에 해당한다
위의 유한 오토마타의 경우, push라는 입력만이 존재하며 알파벳은 push이다.
q0
q0은 시작 상태를 의미하며, 유한 오토마타는 항상 시작 시, 어떤 상태에서 시작할지 표기되어 있다.
화살표의 도착 상태가 유한 오토마톤의 시작 상태를 나타낸다.
F
F는 마지막 상태(final states)를 의미한다.
입력이 끝난 후, FA의 마지막 상태에 있다면 그 문자열은 받아들여진다 판단한다.
그러나, 입력이 끝난 후에 마지막 상태가 아닌 다른 상태에 있게 되면, 그 문자열은 받아들여지지 않는다.
F는 q0와 달리, 여러 개일 수 있다.
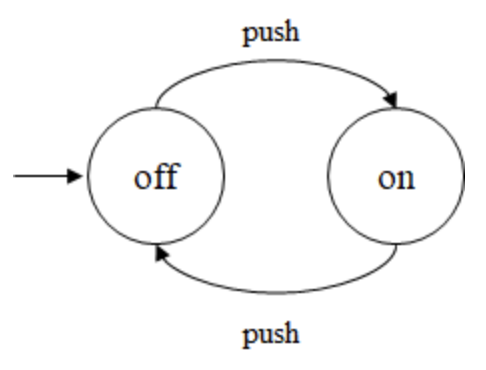
예시의 오토마톤은 마지막 상태가 존재하지 않는다.
위 예시에서 마지막 상태를 표시하려면 다음과 같이 표현하면 된다.
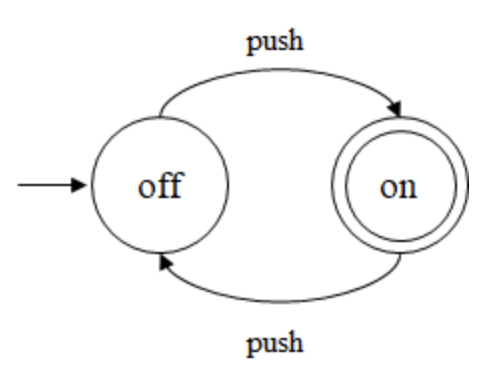
마지막 상태는 다음과 같이 원이 두 개 겹쳐진 형태로 표현한다.
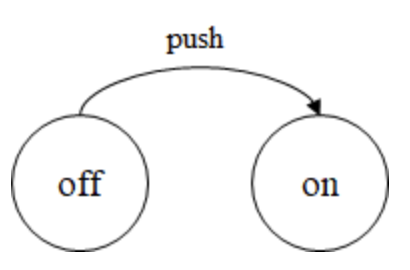
off에서 push라는 입력이 주어졌을때, on으로 전이하는 함수를 다음과 같이 표기한다.
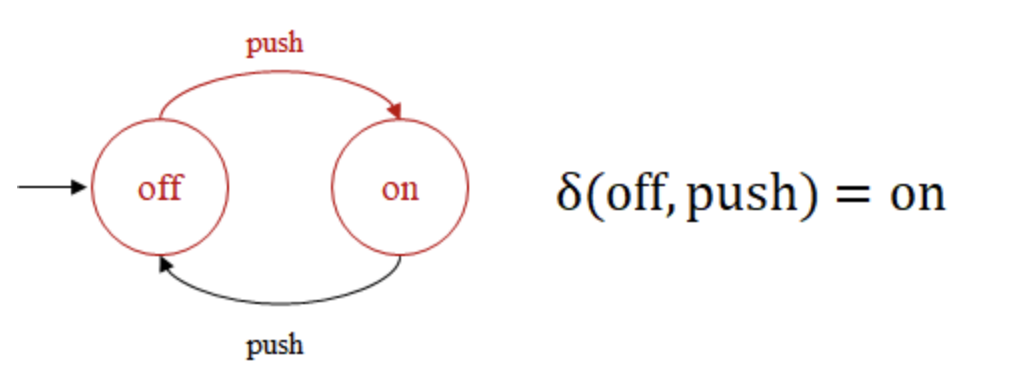
전이 함수의 구성에 따라, 유한 오토마타의 유형이 나눠지게 된다.
유한 오토마타의 유형
유한 오토마타는 3가지의 유형이 존재한다. DFA, NFA, ε-NFA
첫째, 결정적 유한 오토마타(DFA, Deterministic Finite Automata).
둘째, 비결정적 유한 오토마타(NFA, Non-deterministic Finite Automata).
셋째, ε-전이가 있는 비결정적 유한 오토마타(ε-NFA, Non-deterministic Finite Automata with ε-transitions).
유한 오토마타의 유형 구분법 - 1 : DFA vs NFA
❗️어떤 입력 알파벳이 주어졌을때, 전이할 수 있는 경우의 수가 오직 1가지뿐인가?
위 질문에서 그렇다면 DFA, 아니라면 NFA다.
DFA에서는 한 입력에 대해 무조건 하나의 전이만 가능하다. 모든 상태에서 모든 알파벳에 대해 전이 함수가 한가지만 정의되어 있기 때문이다. 이것이 결정적 유한 오토마타(DFA)라고 불리는 이유다. 모든 경우의 수에서 전이가 결정적으로 일어난다.
이와 달리 비결정적 유한 오토마타(NFA)는 한 입력에 대해 여러가지 경로가 존재하거나 아무 경로도 존재하지 않을 수 있다.
example 1
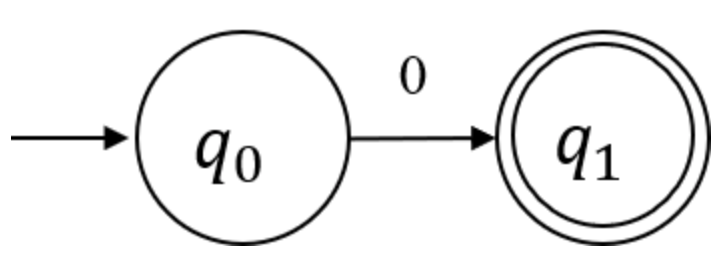
- 상태 : { }
- 알파벳 : { }
- 시작상태 :
- 마지막 상태 :
- 전이함수:
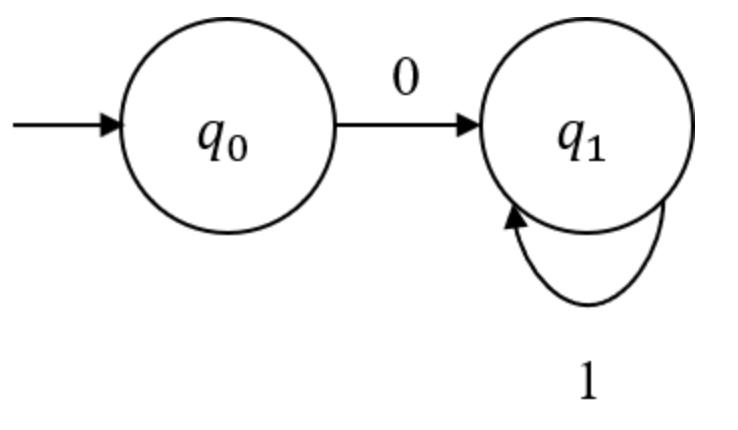
이 유한 오토마타는 전이 함수가 딱 한가지만 존재한다. 위 예시는 NFA다.
왜냐하면 에서는 입력 이 주어졌을때, 전이할 수 있는 경우의 수가 없기 때문이다.
(명시되어있지 않음)
위 예시가 DFA로 바뀌려면 q1에서 입력 0이 주어졌을 때 전이할 수 있는 경우, 한가지를 추가해주면 된다.
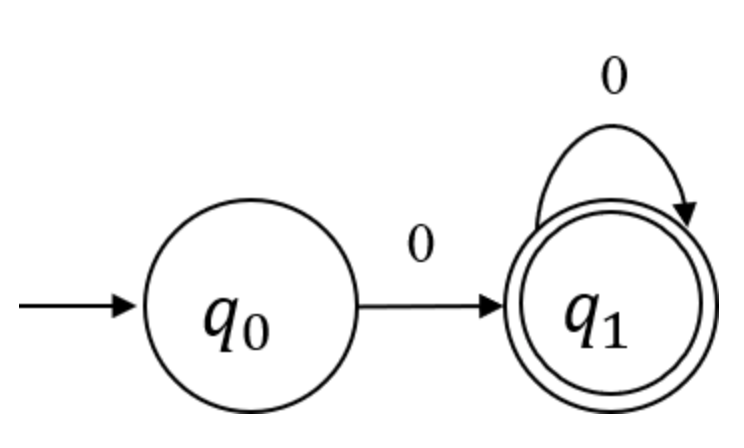
위와 같이 q1에서의 경우의 수가 추가되면 다음과 같이 결정적으로 바뀐다.
example 2
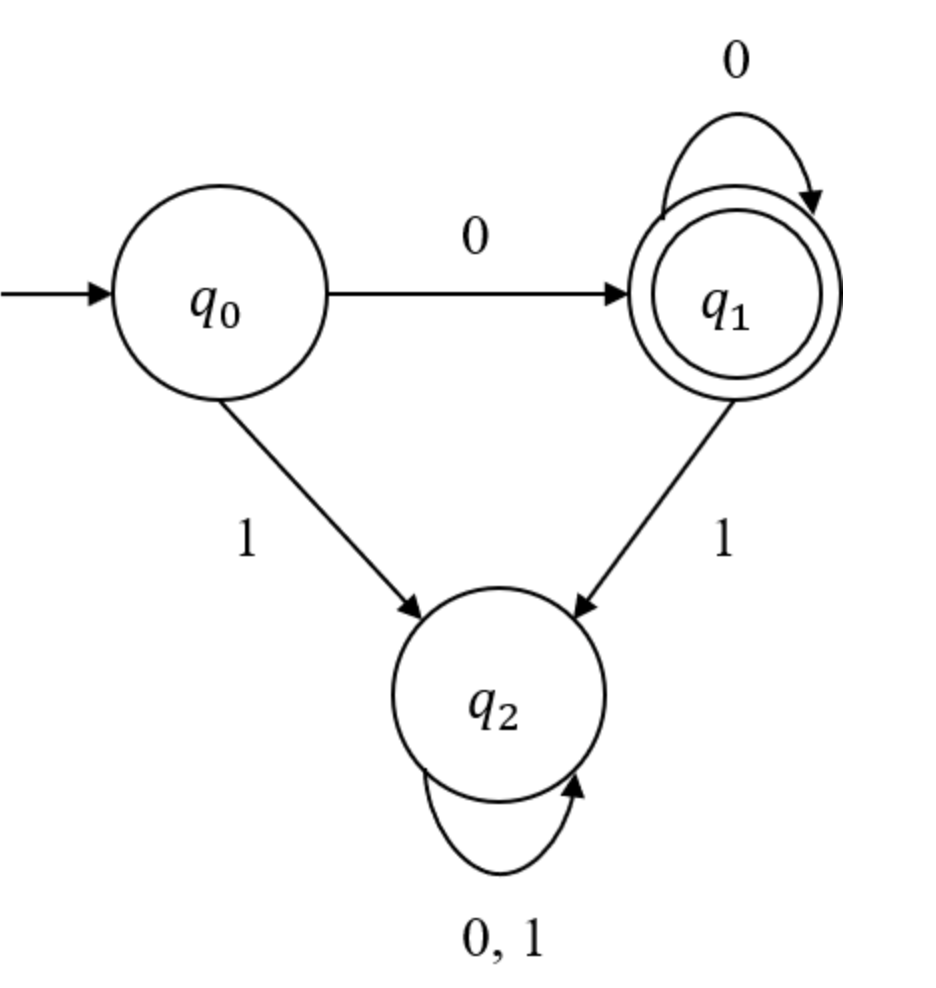
예시를 통해 분석하면, DFA인지 NFA인지 구분가능하다.
- 상태 : { }
- 알파벳 : { }
- 시작상태 :
- 마지막 상태 :
- 전이함수:
해당 유한 오토마타는 모든 상태에서 입력 알파벳 0,1에 대해서 각각 한가지씨 전이함수가 명시되어 있으므로 DFA다.
================================================================
❗️DFA/NFA 구분 방법
1. 입력 알파벳의 개수 확인
2. 어떤 상태를 택해 모든 알파벳에 대해 전이 함수가 한 개씩만 명시됐는지 확인
하나라도 2번을 만족시키지 못하면, 해당 유한 오토마타는 NFA이다.
어떤 입력에 대해 전이함수를 명시하지 않거나, 실수로 두 가지 이상의 전이함수를 정의하게 되면 NFA를 설계한 것이 되어버린다.
위 특성 때문에 DFA의 경우, 총 전이함수의 개수가 정해져있다.
개의 상태와 개의 입력 알파벳으로 구성된 DFA는 개의 전이함수를 가진다.
================================================================
유한 오토마타의 유형 구분법: NFA vs ε-NFA
다음 기준을 통해 NFA와 ε-NFA를 구분가능하다.
=> ε-전이가 존재하는가?
맞다면 ε-NFA, 아니라면 NFA다.
ε-전이
ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ
ε-전이, 앱실론 전이
는 입력이 앱실론인 전이함수를 의미한다.
앱실론은 비어있는 문자열을 뜻한다.
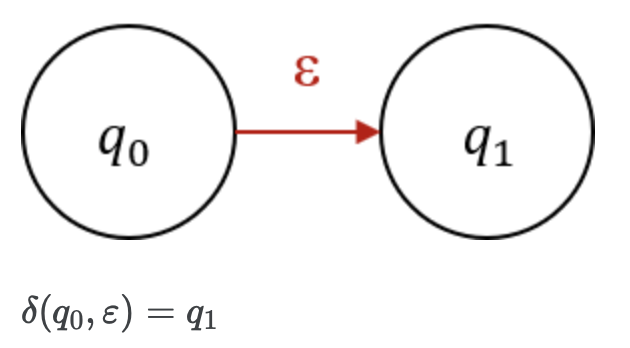
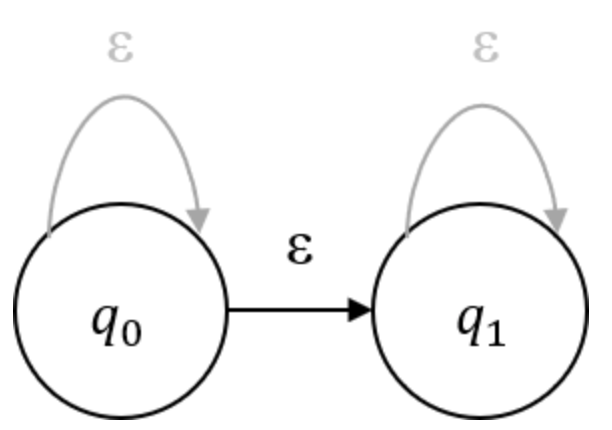
위 사진은 아무 입력도 없어도 q0에서 q1로 전이할 수 있다는 것을 의미한다.
일반적으로는 유한 오토마타에서는 어떤 알파벳이 입력으로 들어오지 않으면, 상태 전이가 이뤄지지 않는다.
그러나 앱실론 전이를 통해 아무런 입력이 없어도 전이가 발생하는 예외적인 상황을 만들 수 있다.
모든 상태는 앱실론이 입력되면, 그 상태를 유지하게 된다.
이는 따로 명시한 앱실론 전이와 달리, 생략된 전이이다.
명시적으로 ε-전이를 정의하지 않은 경우, 암묵적으로 그 상태를 유지하는 것은 앱실론 ε의 성질과 관련이 있는데, 빈 문자열 그 자체를 의미하는 ε은 문자열 어디에나 있을 수 있다.
예를 들어, 011이라는 문자열이 있다면, 앱실론은 문자열의 어디에나 무한하게 존재할 수 있다.
011 = …εεε…εεε0εεε…εεεε1εεε…εεε1εεε…εεε….
앱실론은 무한하게 있지만, 단지 불필요해서 생략된 것 뿐이다.
마치, 5라는 숫자가 있다고 할때 앞뒤에 +0이 무한히 있을 수 있는 것과 같다.
5 = …+0+0+5+0+0+0+…
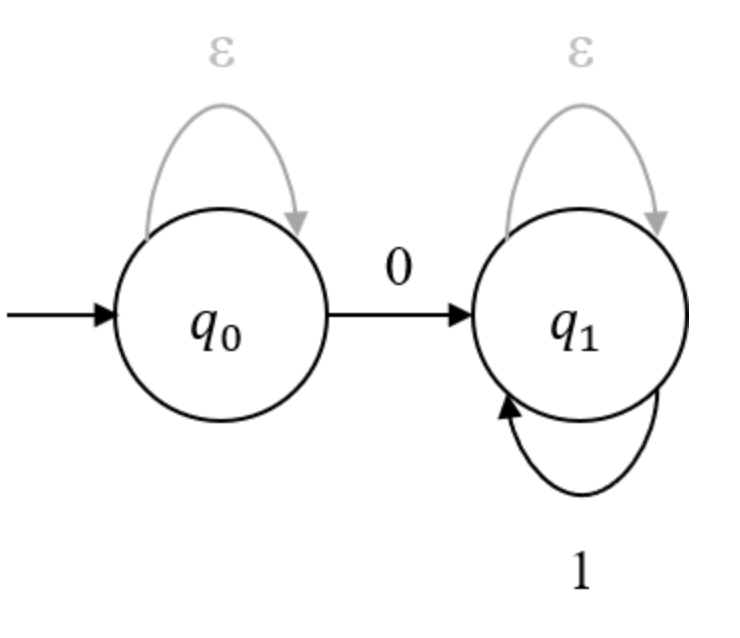
비록 앱실론 전이가 생략됐다한들, 입력을 불문하고 어느 상태에서나 ε-전이가 일어날 수 있다. 때문에 모든 상태는 암묵적으로 제자리걸음하는 ε-전이를 포함하고 있다.
위의 오토마타 또한 실제로는 아래의 앱실론 전이를 포함하고 있는 것이다.
오토마타가 정확히 어떤 상황에 쓰여야하는지 잘모르겠지만, 기회가 되면 추가로 정리해서 포스팅할 생각은 있다.
앱실론 전이가 특정 언어 인식에 유용하게 사용될 수 있다는 것은 인지하게 됐다.
'책벌레와 벌레 그 사이 어딘가 > 개념쌓기' 카테고리의 다른 글
| [개념쌓기] 오토마타 - 2 (49) | 2024.01.15 |
|---|---|
| [개념쌓기] 오토마타 - 1 (29) | 2024.01.03 |
| [개념쌓기] 메타데이터(Metadata)란? (77) | 2023.12.07 |
| [개념쌓기] CAN & ETH (71) | 2023.11.28 |
| [개념쌓기] 데이터 직렬화(Serialization) (124) | 2023.10.26 |
댓글